MLR is a technique in statistics that employs a variety of explanatory variables to determine the results of an outcome variable. Multiple linear regression describes the relationship between explicatory (independent) variables and the response (dependent) variables. It is an extension of the standard least-squares (OLS) regression since it includes more than one explanatory variable.
What Can Multiple Linear Regression Tell You?
A simple linear regression technique lets an analyst or statistician make predictions about a particular variable based on available data about another variable. Linear regression can be utilized when there are two continuous variables: independent and dependent variables. The Independent variable acts as the variable used to calculate the dependent variable or outcome. The model of multiple regression extends to several explanatory variables. The model for multiple regression is built on some of the assumptions below:
- The linear connection between the dependent variables and the independent variables.
- The independent variables aren't significantly correlated with each other.
- The observations of yi are chosen by random selection from the general population
- Residuals must be distributed normally with a mean of zero and a variance σ
The coefficient of determination (R-squared) is a measure that is used to assess the extent to which variance in outcomes can be explained by variations in the variables that are independent. R2 increases every time, increasing the number of predictors in the model of MLR, regardless of whether the predictors may not be connected to the outcome variable.
R2 on its own cannot, therefore, be used to determine which predictors are appropriate to include in a model and those that should be omitted. R2 can only be between one and zero, in which 0 indicates that the result cannot be predicted by one of the dependent variables, and 1 means that those variables can predict the result with confidence.
How to Utilize
For instance, an analyst might be interested in knowing how the performance of the market impacts the pricing of ExxonMobil (XOM). In this scenario, their linear equation will be based on the S&P 500 index as the independent variable or predictor for the price of ExxonMobil (XOM) as the dependent variable.
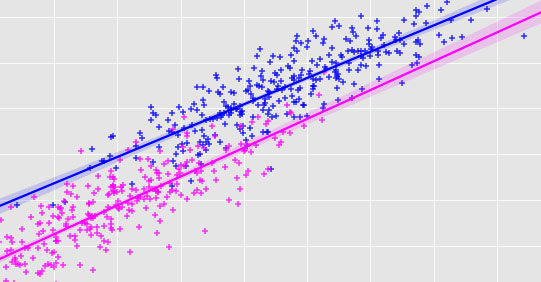
In reality, many variables can determine the outcomes on the day of the event. The price of ExxonMobil, for instance, depends on more than the performance of the entire market. Other variables that can be used to predict price, like the rate of interest, the cost of oil, and the price of oil futures, could influence the prices of XOM and the stock rates of oil-related companies. The multiple linear regression method analyzes a relationship where more than 2 variables are in play.
Multiple linear regression (MLR) is utilized to establish the mathematical relation between various random variables... When each independent variable has been identified to determine that dependent variable, data about the different variables can be used to estimate their influence on the result variable. The model establishes a relationship that is straight lines (linear) which is the most accurate representation of each data point.
Linear and Multiple Regression
In OLS regression, the responses to a variable are compared after being subjected to a change in the explicatory variables. On the other hand, a dependent component is seldom described by a single independent variable alone. In this particular scenario, researchers use a technique known as multiple regression to explain a dependent variable based on several independent factors. Both linear and nonlinear approaches are valid for doing multiple regressions.
When doing multiple regressions, the assumption that the dependent and independent variables are connected linearly is used as the foundation. Additionally, the model presupposes no meaningful link between the independent variables.
What Makes A Multiple-Regression Different?
Multiple regression analyzes the influence that more than one explanatory variable on a particular outcome that is of importance. It analyzes the effect of these explicatory or independent variables upon the dependent variables while keeping all other variables of the model as constants.
Multiple Regression Models Used In the Finance
Every model in econometrics that analyzes more than one variable could be multi-variable. Factor models evaluate two or more variables to determine the relationship between variables and their performance. For instance, the Fama three-factor model, also known as the French one, is an example of the model that extends the capital asset pricing model (CAPM) by including size risk and value risks to the market risk component of the model (which is itself an equation model). In addition to these two factors, the model can be adjusted to account for this outperforming tendency which could create a more effective tool to assess managers' performance.



